Study on the dynamic properties and application of TiZrTaMoNb high-entropy alloy

0 Introduction 

Since the discovery of the polyenergy effect by Munroe [1] in 1888, polyenergy charges have been widely used in the combat sections of munitions and engineering fields. After several centuries of development, the application of poly energy charge in the combat part is now mainly divided into three types: poly energy jet (JET), poly energy rod projectile (JPC), and explosively formed projectile (EFP).

The molding and destructive effect of the poly energy charge is affected by a number of factors such as the material of the drug mask, the charge structure and the shape of the drug mask. Currently, the research on EFP materials mainly focuses on the following two aspects: one is to explore the feasibility of applying new materials to EFPs; the other is to optimize the production process of commonly used EFP materials in order to improve the performance of EFPs. In the study of the feasibility of new materials applied to the drug mask, the main consideration is density, speed of sound, physical symmetry and geometric symmetry of the four basic elements [2]. Compared with JET and JPC, the deformation of the EFP battle section in the molding process tends to be relatively small, less likely to occur similar to the extreme deformation of the fluid in general, so the EFP battle section for the ductility of the drug mask material requirements are also slightly lower accordingly. In the EFP combatant penetration process, often approximated as a kinetic energy bomb for processing, the density and strength of the material has high requirements. Therefore, in the specific requirements for the selection of material for the drug-type cover, EFP combat part and JET and JPC have some differences.

High-entropy alloys (High-entropyalloys), also known as multi-major element alloys, can be used to achieve the ability to regulate important parameters such as density, ductility, strength, energy content, etc., through the atomic level proportioning of different components. In view of the excellent performance of high entropy alloys, some scholars have studied the application of high entropy alloys in the combat unit, some of which will be used as the combat unit shell material [4] or kinetic energy projectile material [5-6], and some scholars will be used as a lightweight high entropy alloys as a poly energy jet medicine type cover material [7], have achieved better results. The TiZrTa-MoNb high entropy alloy studied in this paper is a Ti-Zr refractory high entropy alloy made by equal atomic ratio, with a density of 9.118g/cm3, which is comparable to that of the current commonly used material for drug masks-copper (8.9g/cm3), and the yield strength of the Ti-Zr refractory high entropy alloy is about 1,000 to 2,000MPa [3], but due to the incorporation of Mo and Mo, the material has been used as the material for the kinetic projectile [7]. According to the quasi-static compression test results, the yield strength of TiZrTaMoNb high entropy alloy in static compression is about 859MPa. From the above data, its strength and density meet the basic requirements as the material of the EFP drug mask, and due to the lack of tensile test, it is not possible to make a more intuitive evaluation of the ductility of TiZrTaMoNb high entropy alloy. The ductility of TiZrTaMoNb high-entropy alloy cannot be evaluated intuitively due to the lack of tensile experiment. Therefore, the ductility of TiZrTaMoNb high-entropy alloy is roughly estimated by combining the elongation at break of several high-entropy alloys of the same type with the failure strain parameter in the compression experiment.

According to the existing reports, TaNbTiZr refractory high-entropy alloys [8] fracture elongation is about 3.99%; equal atomic ratio of TiZrNbHfTa high-entropy alloys [9] yield strength, ultimate fracture strength of 1170, 1260 MPa, respectively, the fracture elongation of 8%, showing excellent strength-plastic synergistic effect; by Juan et al. [10] to prepare HfMoN- bTaTiZr refractory high-entropy alloy can still maintain 12% fracture elongation at room temperature and increase with the temperature, reaching 30% at 1200℃, showing more obvious temperature softening phenomenon. According to the results of static and dynamic compression experiments, TiZrTaMoNb high entropy alloy in quasi-static compression, the failure strain is about 29.4%; in the dynamic compression experiments, when the strain rate rises from 851s-1 to 2403s-1, the maximum strain rises from 12.6% to 33.8%, and the specimen does not produce cracks in the process. The specimens did not produce cracks and showed good ductility.

Comprehensive static and dynamic compression test results and the above scholars research content, TiZr-TaMoNb high entropy alloy exists as the possibility of the material of the drug mask, so the TiZrTaMoNb high entropy alloy used in the feasibility of the EFP drug mask material was studied.

1 Experimental study 

1.1 Experimental setup

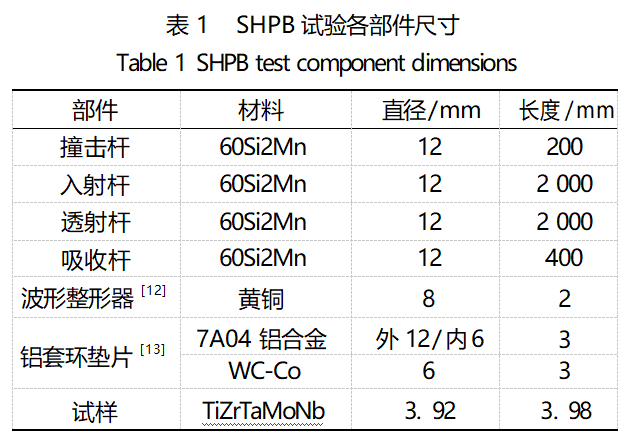
The quasi-static compression test was conducted using a universal testing machine with a strain rate of 0.001s-1 and a sampling frequency of 1MHz.The dynamic compression test was carried out using SHPB, and the setup was carried out with reference to literature [11]; a total of four groups of dynamic compression tests were carried out, and the sketch of the SHPB test is shown in Fig. 1, and the dimensions of the test parts and materials are shown in Table 1.

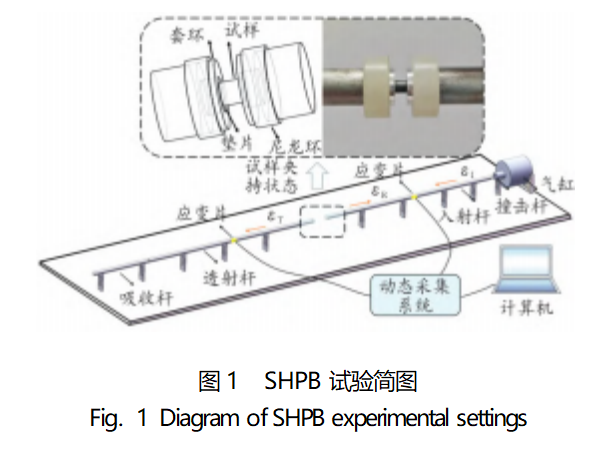
1.2 Test results and data processing 

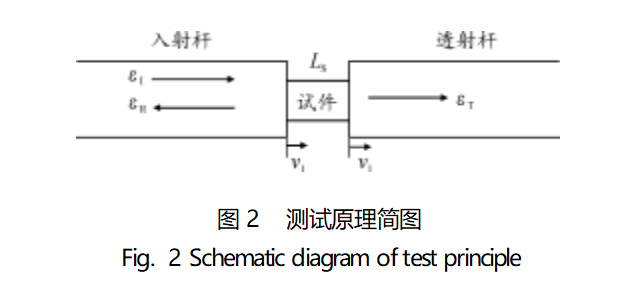
The SHPB test test principle is shown in Figure 2, when the specimen is in stress equilibrium, the average engineering strain rate and strain are calculated by Eq. (1) and Eq. (2): 

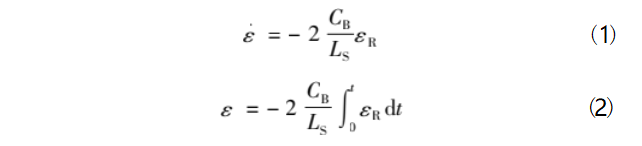
where: LS is the initial length of the specimen; v1, v2 are the incident rod, transmission rod mass movement velocity, respectively; εI, εR, εT are the incident wave, reflected wave and transmission wave, respectively; CB is the rod material; εT is the incident wave, reflected wave and transmission wave, respectively. wave; CB is the wave speed of the rod material.

The stresses at both ends of the specimen are calculated by the following elastic relations [14]: 

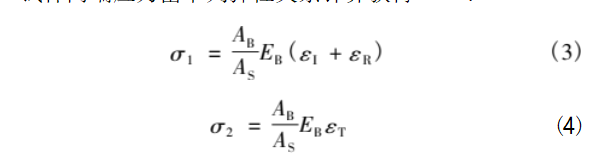
where:AB, AS are the cross-sectional area of the rod and specimen respectively; EB is the elastic modulus of the rod material.

The test results were processed by the above equation, and the stress-strain curves at each strain rate were plotted as shown in Fig. 3, and the yield strength, maximum stress and maximum strain are listed in Table 2. 

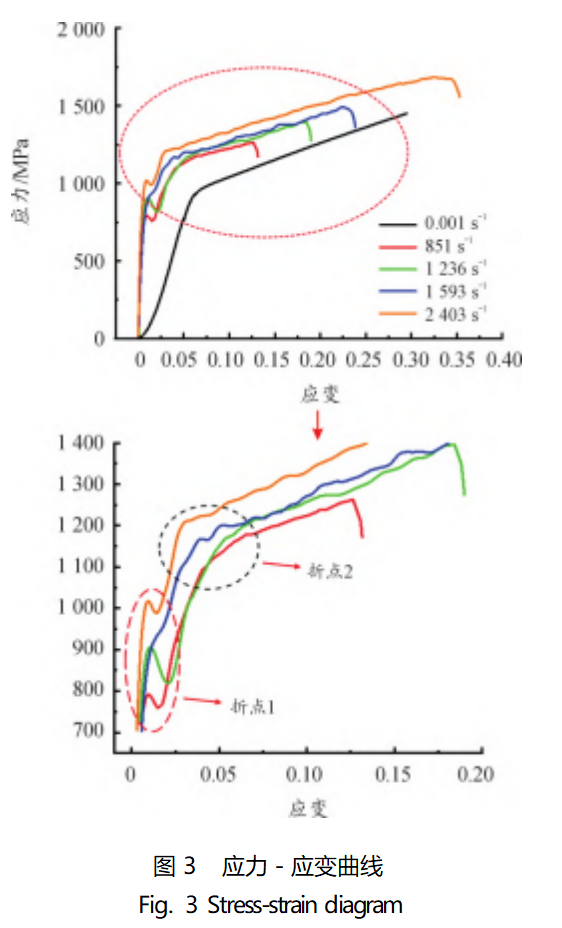
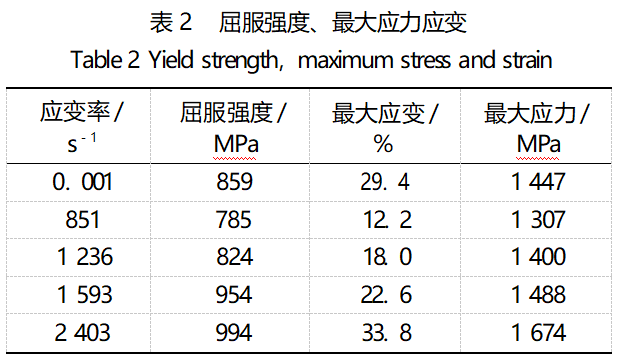
From Fig. 3, it can be seen that, when the strain rate is increased from 851s-1 to 2403s-1, the yield strength increases from 785 MPa to 994 MPa, and the maximum strain increases from 12.2% to 33.8%, reflecting a more obvious strain rate effect.

2 The fitting of the parameters of the intrinsic model 

2.1 Selection of the intrinsic model 

EFP molding is a high strain rate process, and it is necessary to select a suitable material model to describe the stress-strain relationship and the strain rate effect of the material under the condition of high strain rate. The Johnson-Cook model [15] encompasses the effects of the strain, strain rate and temperature on most of the metallic materials, because of its simple form, physical and chemical properties, and it can be used as a model of the material. The Johnson-Cook model [15] encompasses the effects of strain, strain rate and temperature factors on most metallic materials, and is widely used in the field of explosions and shocks because of its simple form, clear physical meaning, and easy to test and calibrate parameters. Therefore, the Johnson-Cook model is chosen to describe the stress-strain relationship of TiZrTaMoNb high-entropy alloy in the case of impact response, and this constitutive model is defined by three multiplicative terms of strain-hardening, strain-rate sensitivity and temperature, which are defined as follows: 

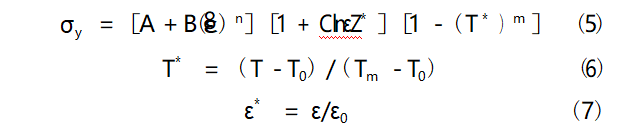
where: is the equivalent plastic strain, ε* is the dimensionless plastic strain rate, ε0 is the reference 

strain rate (reference strain rate taken quasi-static loading strain rate); T* for the relative temperature, T0 for the reference temperature (generally room temperature), Tm for the melting temperature, T for the instantaneous temperature. A, B, n, C, m for the parameters to be fitted.

2.2.2 Parameter fitting of the intrinsic model 

2.2.1 Parameter fitting method 

The three parameters A, B, n describe the stress-strain relationship at the yield point and the plastic deformation stage of the material at a fixed strain rate. Generally, A, B and n are fitted according to the stress-strain curves under quasi-static, room temperature loading conditions. Under quasi-static loading condition, the strain rate is 0.001s-1, and room temperature is taken, therefore, equation (5) can be simplified as 

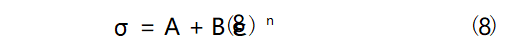
At the initial yield point, this time can be regarded as plastic strain has not yet occurred, ε=0. At this time, A is the yield strength, and the value of B, n can be determined by fitting the stress-strain curve for the plastic stage.

C can be determined by fitting the yield strength values corresponding to different strain rates at room temperature, at which time the equation becomes 

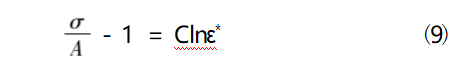
2.2.2 Parameter fitting results 

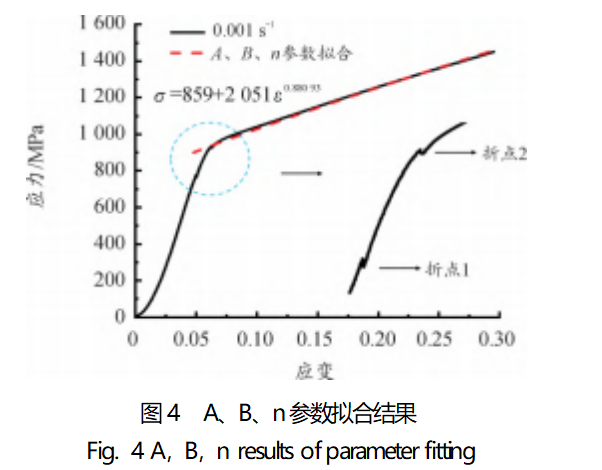
The strain rate under quasi-static loading conditions at room temperature is taken as the reference strain rate (0.0. 001s-1), and the parameters 

A, B, n are fitted to the stress-strain curve of the plastic stage under the reference strain rate, and the results are shown in Fig. 4. The fitting results are shown in Fig. 4.

As can be seen in Fig. 4, the yield strength of TiZrTaMoNb high-entropy alloy under quasi-static loading at room temperature (strain rate 0.001s-1) is 859 MPa, i.e., the value of A is 859 MPa. Fixing the value of A, the plastic phase of the stress-strain curve is fitted to obtain the parameter B is 2051 MPa, and the value of n is 0.88093. 88093. 

According to Eq. (9), the parameter C is fitted by using the method of determining the yield strength of the dynamic compression test with a single thread, and the fitting results are shown in Fig. 5.

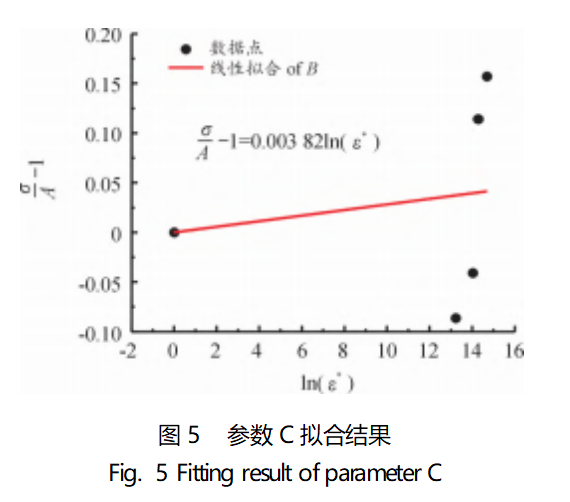
As can be seen from Fig. 5, the slope of the fitted curve is 0.00382, i.e., the parameter C is 0.00382. Since the fitting process ignores the influence of temperature change on the strain effect of the material, the equations of the intrinsic model (ignoring the temperature term) are shown as follows: 

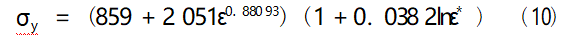
As can be seen in Fig. 5, the linearity of the fitting results for the parameter C is poor. It can be seen from Fig. 5 that the linearity of the fitting result of parameter C is poor, in order to make a rough estimation of the validity of parameter C, several strain data points are selected and substituted into Eq. (10) for calculation, and the calculated results are compared with the experimental curves and plotted as shown in Fig. 6.

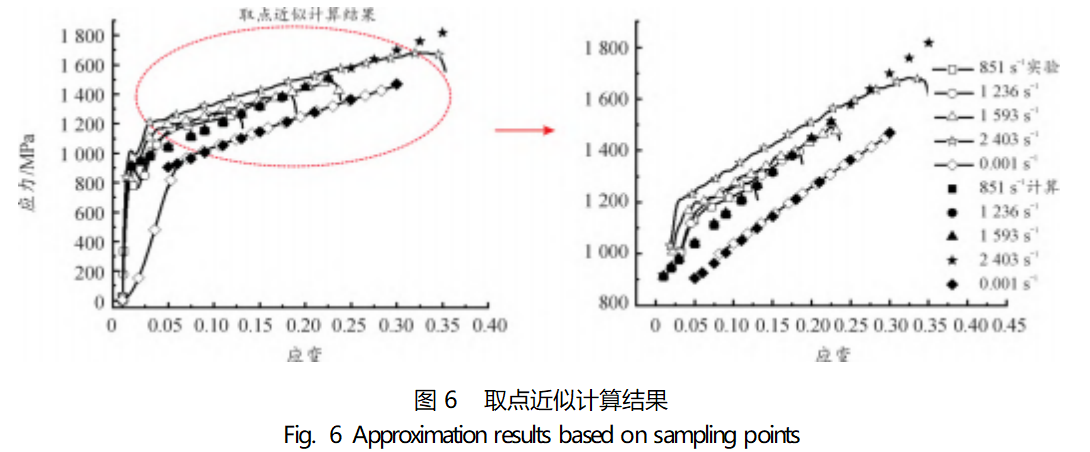
As can be seen from Fig. 6, there is a large gap between the results calculated using the fitted parameter taking points and the curve obtained from the experiment, which cannot reflect the strain rate effect of the material. It can also be seen from Fig. 5 that the degree of relationship between the linearly fitted curve for parameter C and each data point is poor, and the linearly fitted curve cannot represent the stress-strain situation for each strain rate. It is mainly manifested in the fact that the approximate calculation results of each strain rate do not have much difference and seem to be “crowded” together. The main reason for this situation is that the parameter C that controls the strain rate effect is not accurate enough to truly reflect the strain rate effect of the material.

According to equation (9), parameter C reflects the linear relationship between the ratio of yield strength under each strain rate and reference strain rate and the ratio between each strain rate and reference strain rate. The parameter C is jointly influenced by the reference strain rate, each dynamic compression test strain rate, the yield strength A under the reference strain rate and the yield strength σ under each dynamic strain rate. As can be seen from Figs. 3 and 4, whether it is dynamic compression or static compression, there are 2 folding points in the stress-strain curve; and it is more obvious that dynamic compression in the elastic section after there is a period of strengthening stage, not directly into the plastic deformation stage, in this stage, the stress and strain are still more obvious changes, if you use a single-threaded method to determine the yield strength, it will lead to the yield point after the yield point is directly into the plastic deformation stage, missing the stress changes in the strengthening stage, resulting in small stresses, as shown in Fig. 6.

In order to solve this problem, the parameter C was re-fitted using the bilinear method of determining the yield strength, and the results of the bilinear method of determining the yield strength are shown in Table 3.

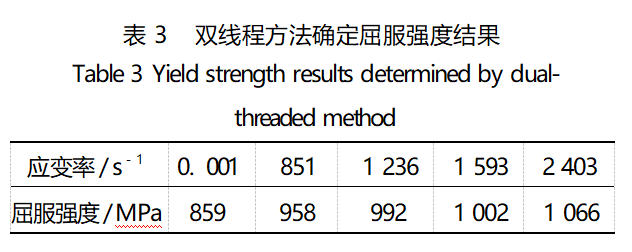
The results of the refitting of parameter C are shown in Fig. 7, and the results of the calculation of the points taken after the refitting of parameter C are shown in Fig. 8.

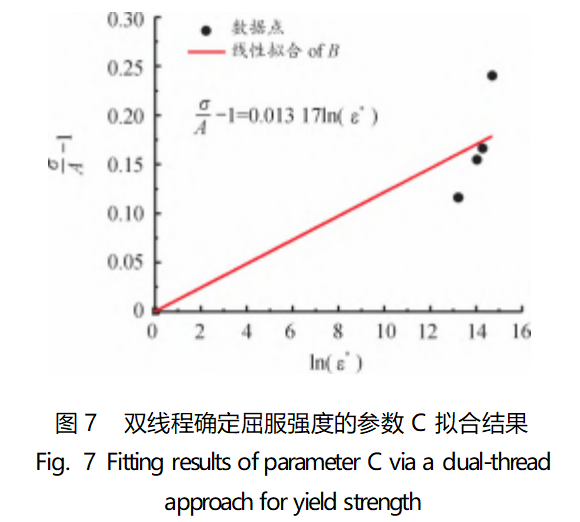
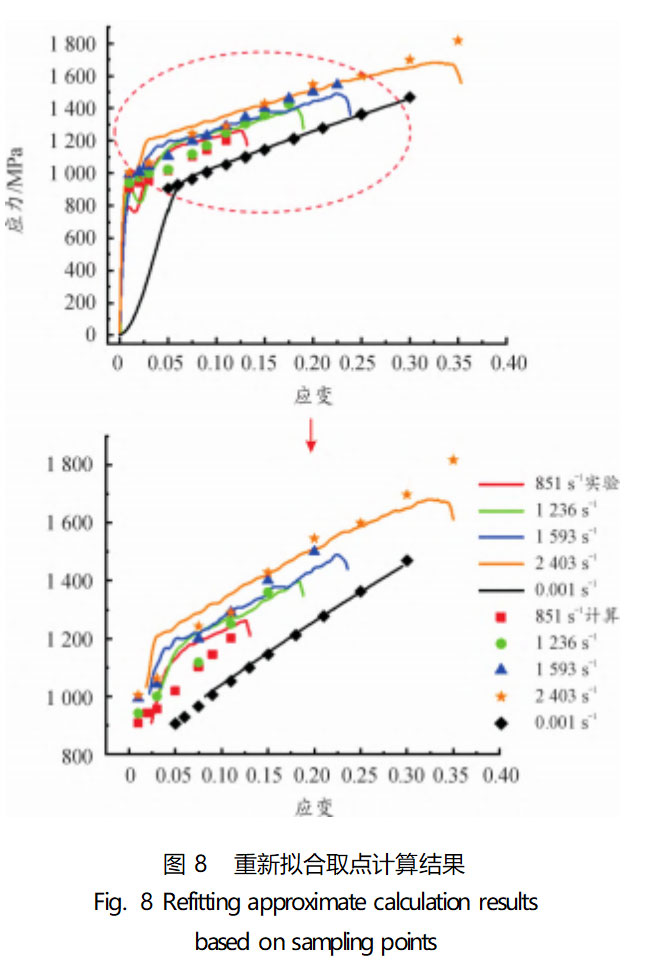
Comparing Fig. 7, Fig. 8 and Fig. 5, Fig. 6, it can be seen that the linearity of parameter C after refitting as well as the results of the approximate calculation are better than the original, closer to the experimental effect, and can reflect the strain rate effect of the material. The re-fitted constitutive model equations are shown in Eq. (11).

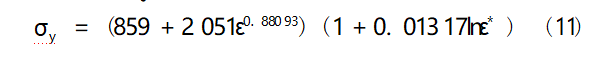
2.3 Equation of state parameter fitting 

The Grunisen equation of state is used to describe the change of state of the material when it is subjected to shock waves. The equation of state takes into account the nonlinear and nonequilibrium properties of the material under shock wave loading, as well as the influence of high temperature and high pressure, which can effectively characterize the state change of the material. Under shock loading, the relationship between the propagation velocity of the shock wave front and the rear particle motion velocity in the material can be expressed by equations (12) and (13).

 where:U is the propagation velocity of the shock wave front, C0 is the body sound velocity of the material at room temperature, S is the linear Hugoniot gradient, and up is the velocity of the particle motion behind the wave.

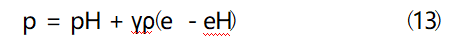
 where:γ=B0/(1+μ), μ is the Poisson's ratio of the material, and B0 is a constant; pH is the Hugoniot pressure; eH is the Hugoniot energy.

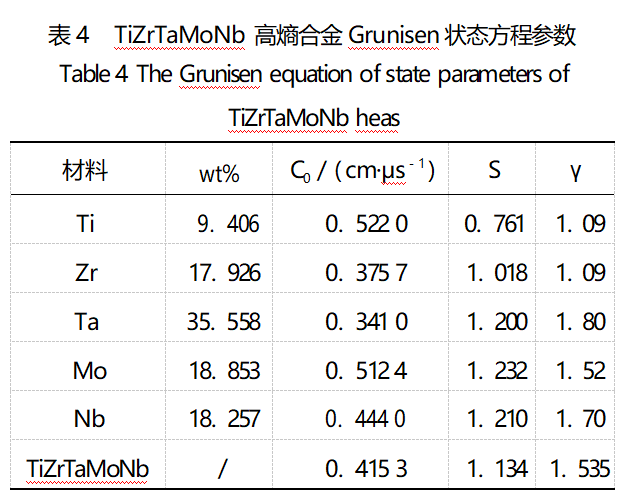
Due to the lack of flat plate impact tests related to TiZrTaMoNb high-entropy alloys, the parameters of the Grunisen equation of state of TiZrTaMoNb high-entropy alloys were approximated using the Voigt-Reuss-Hill [16-17] mixing rule, which was calculated as shown in Eq. (14). The Grunisen equation of state parameters of TiZrTaMoNb high entropy alloy calculated by each metal monomer and approximation are shown in Table 4 below.

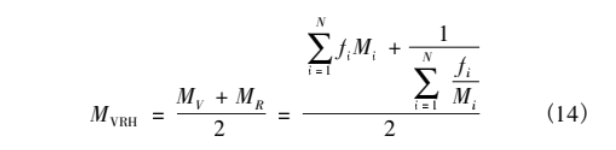
where:fi is the mass fraction of the component;Mi is the parameter of each component.

3 Model validation 

3.1 Numerical model 

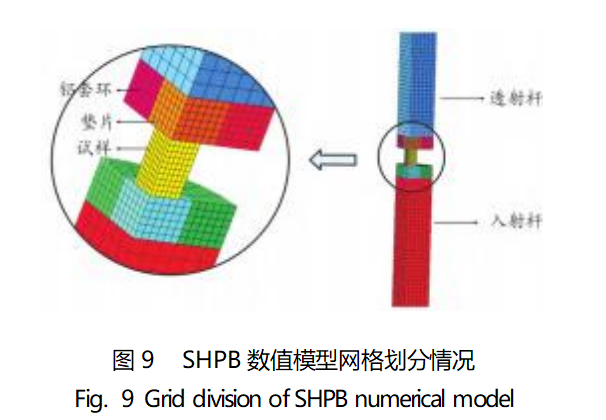
To verify the accuracy of the fitted parameters, numerical simulations were performed using LS-DYNA finite element simulation software. A 1/4 3D finite element model was established according to the SHPB test equivalent scale, and (SURFACE-To-SURFACE) face-to-face contact was used between the end faces, and the model was meshed using 3DSolid164 hexahedral cells, and the meshing was shown in Figure 9.

From the SHPB test theory, it is known that the incident wave propagates as an elastic wave in the rod [14], therefore, Eq. (15) is chosen to transform the voltage signal measured by the strain gauge into a stress-time change curve loaded onto the model.

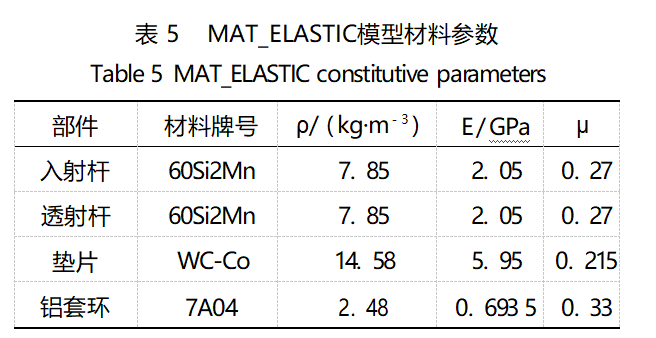
where the steel rod, gasket and aluminum collar are selected MAT_ELASTIC material model, the main material parameters are shown in Table 5. TiZrTaMoNb high entropy alloy specimens are selected Johnson-Cook intrinsic model, with Gruneisen equation of state, the main material parameters are shown in Table 6.

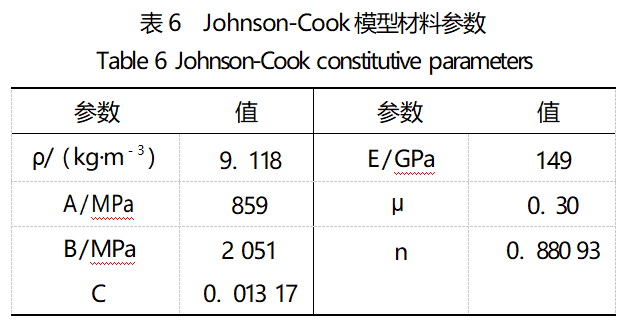
Note:ρ is the density; E is the elastic modulus; μ is Poisson's ratio; A, B, n, C are the fitting parameters; εZ0 is the reference strain rate.

3.2 Numerical simulation results 

The stress-time variation curve of the incident wave calculated according to Eq. (14) is shown in Fig. 10. The incident wave was loaded onto the end face of the incident rod, and numerical simulation was carried out to verify the four dynamic compression tests (strain rates of 851, 1236, 1593, and 2403 s-1), and the stress-strain curves obtained from the numerical simulation are shown in Fig. 11.

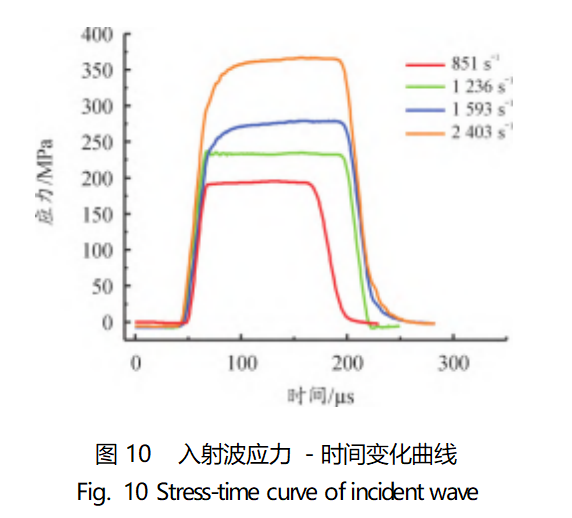
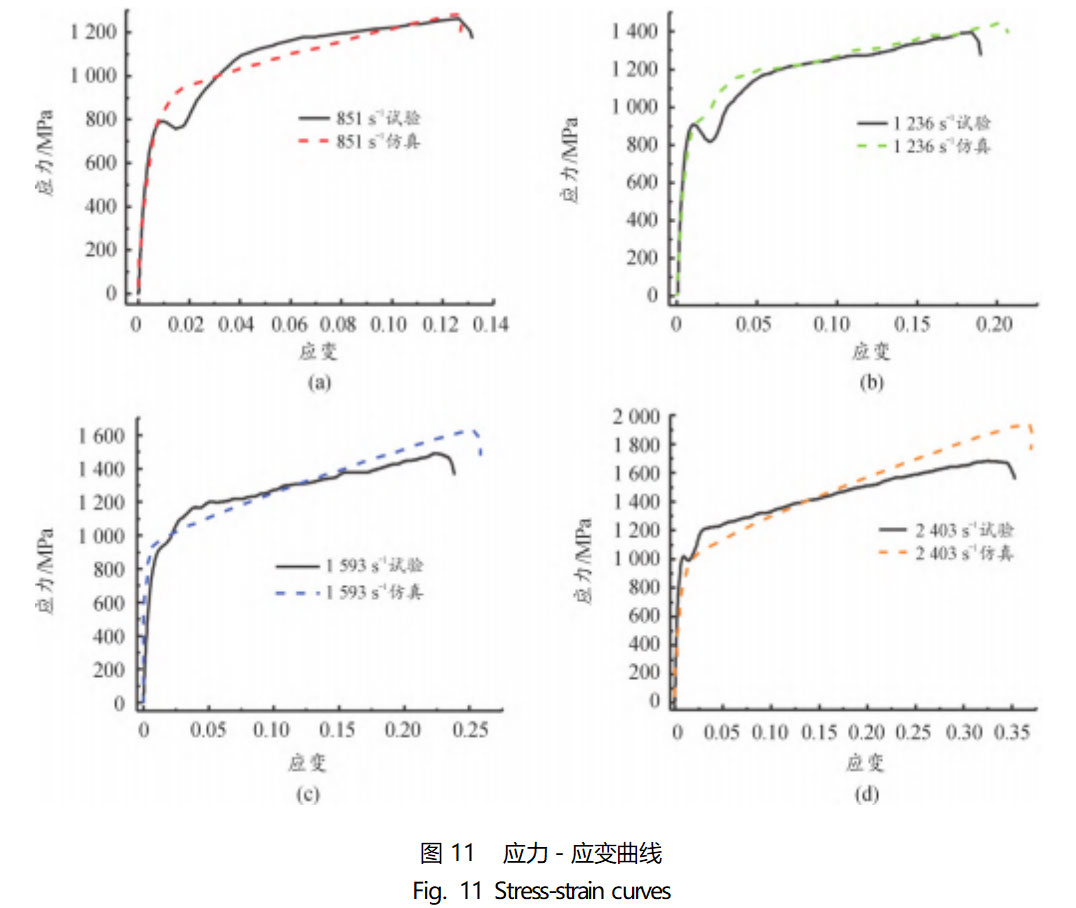
As can be seen from Fig. 11, there is always a certain error between the stress-strain curve calculated by the simulation model and the test, and the error mainly comes from the following three aspects: first, in the curve obtained from the test data, there is a more obvious strengthening phase after the yield point, and the use of the Johnson-Cook material model fails to reflect this change; second, the static compression (1236, 1593, 2403s-1 ) is the most important factor in the stress-strain curve. Second, the slope of the curves in the plastic deformation stage of static compression (0.001s-1) and dynamic compression is inherently different, and this difference directly leads to the A, B, n parameters obtained from the reference strain rate fitting in the simulation of high strain rates will appear a certain amount of error; third, the strain rate enhancement effect in the impact of the stress change is not obvious, which is due to the parameter C in the There is also some error in the fitting process.

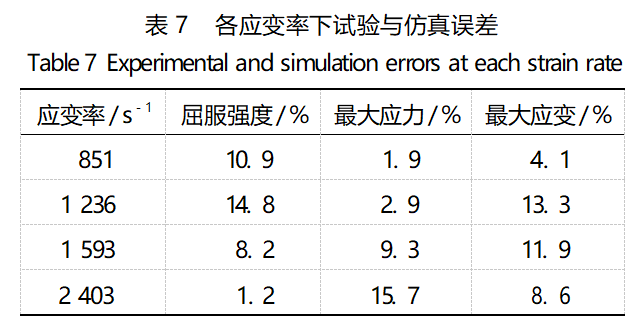
The three parameters of yield strength, maximum stress and maximum strain are selected as the indexes for calculating the error, and the error between simulation and test under each strain rate is calculated and listed in Table 7. 

4 EFP molding simulation test 

4.1 EFP simulation model 

Researchers have been committed to finding materials with both high ductility and high strength in order to satisfy the requirements of both molding of polymerized charges and the effect of intrusion at the same time. High-entropy alloys have excellent properties such as high hardness, high strength, and good thermal stability due to their multi-major element composition and simple solid solution structure, which have the possibility to be used as munition combat part materials. In order to study the feasibility of TiZrTaMoNb high entropy alloy applied to EFP, the EFP finite element model is established, and several common flux mask materials are selected (Table 8), and the molding effects of TiZrTaMoNb high entropy alloy and common materials are compared.

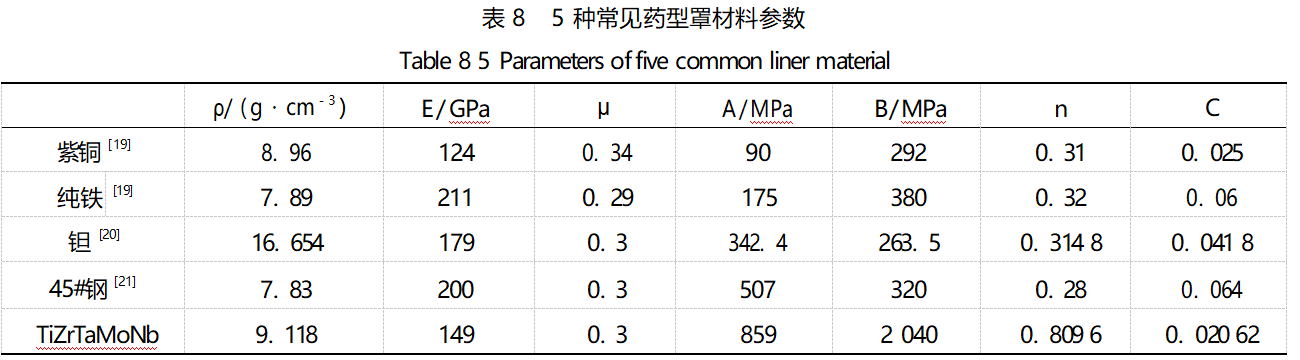
calculation using the drug mask for the variable wall thickness of the ball missing type cover, cover the top wall thickness δ = 0.25 

cm, inside and outside the radius of curvature were 7.73, 7.13 cm. The use of cylindrical charge, the end of the boat-tail shape, the charge diameter D = 7.5 cm, the charge aspect ratio L / D = 1; the use of JH-2 explosives (8701), the charge density of 1.71g/cm3 [18]; the establishment of 1/4 symmetric model is shown in Figure 12.

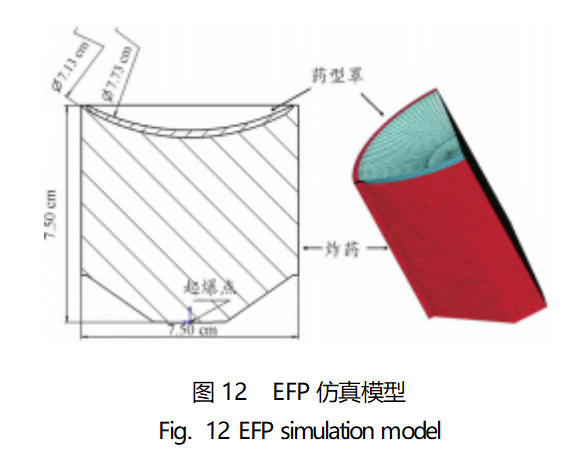
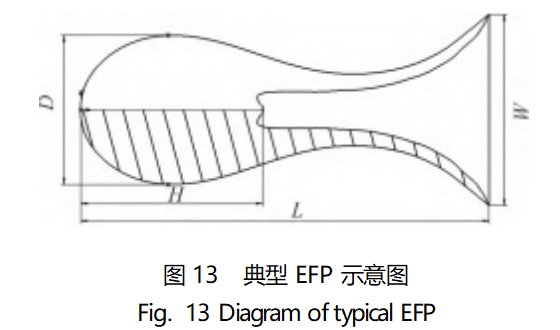
In order to compare the EFP molding effect of the above five materials, the concepts of “length-to-diameter ratio” and “compactness” are introduced [22-23]. Typical EFP is shown in Figure 13: EFP projectile can be divided into the front end of the dense head and rear end of the hollow tail 2 parts; D refers to the maximum diameter of the head, L is the full length of the projectile, H is the length of the dense head; L/D is used to characterize the aspect ratio of the EFP, H/L is used to characterize the degree of compactness of the EFP.

4.2 Analysis of simulation results 

The molding process of EFP for five materials is shown in Fig. 14. Forming process, in 25μs when the explosives have completed the blast, after which the explosives have little effect on the deformation of the drug mask, the EFP molding depends mainly on the self-forgery behavior of the drug mask, so the restart analysis can be used to delete the explosives part, to avoid because of the explosives lattice distortion caused by the calculation of the interruptions; in the 25-100μs, the drug mask continues to deform, the formation of the final shape of the EFP projectile. The more obvious changes are: under the action of the blast wave, the surrounding microelements converge to the top of the hood and gradually stretch and lengthen under the action of the velocity difference, eventually forming a dense head, and the edge part gradually converges to the axis to form a tail.

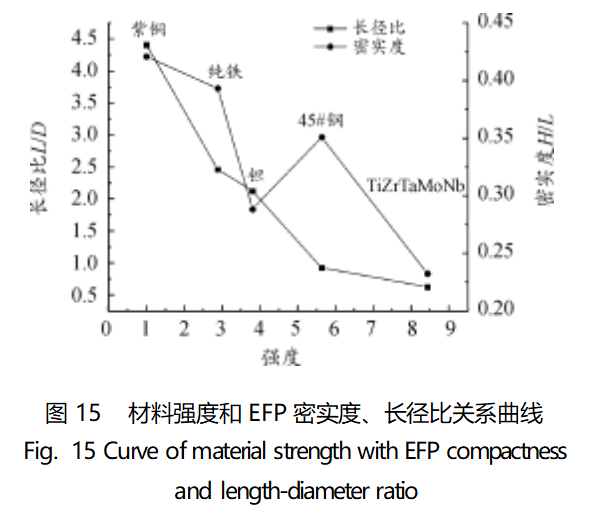
The ratio of the yield strength of each material and copper represents the strength of the material, and the relationship curve between the strength of the material and the length-to-diameter ratio and the degree of densification is plotted as shown in Fig. 15.

Combined with Figures 14 and 15, it can be seen that all other conditions being equal, the EFP projectiles formed from the lower strength copper, pure iron and tantalum have relatively higher aspect ratios and densities relative to both 45# steel and TiZrTaMoNb, forming elongated projectiles with higher densities in the head. For the higher strength 45# steel and TiZrTaMoNb alloy, both the aspect ratio and compactness are relatively low, and they tend to form hemispherical projectiles with lower compactness. It can be seen that as the strength of the material rises, the molding effect becomes worse and worse; there is a negative correlation between the aspect ratio, the degree of compactness and the strength of the material.

The TiZrTaMoNb high entropy alloy studied in this paper is poorly molded under the current shape of the pill hood, with low aspect ratio and compactness, and its molding mode is a forward-turned shape. The main reasons for this are:the material strength is high, the height of the top of the spherically deficient hood is small, the material strength is dominated by the strain rate effect is low under the loading of the blast wave; the radial compression velocity of each microelement in the molding process attenuates faster, and the surrounding mass can not be converged to the top of the hood under the action of the radial velocity; and the axial velocity gradient is small, and the inner and outer wall velocity difference is not obvious, so that the top of the hood can not be stretched to become a slender and Dense head. As a result, by changing the height of the top of the hood, increase the radial compression velocity and axial velocity gradient of each micro-element, so that the micro-elements to the top of the hood to converge and stretch to form the EFP projectile with a high aspect ratio and compactness.

4.3 Optimization of the structure of the drug-type cover 

The factors that affect the molding effect of the variable wall thickness ball lack of cover are mainly: cover top wall thickness, cover top height, cover wall thickness gradient, and the charge length-diameter ratio. In the case of constant loading conditions, the molding effect of the EFP projectile is mainly affected by the shape parameters of the mask, while the height of the top of the mask and the wall thickness gradient of the mask are determined by the inner and outer curvature radii. Therefore, the optimization of the EFP projectile forming effect can be achieved by adjusting the radius of curvature inside and outside of the ball-shaped hood.The following relationships exist between the length-to-diameter ratio and compactness of the EFP projectile and the radius of curvature inside and outside of the hood: the compactness of the EFP projectile is positively correlated to the inner radius of curvature of the hood and negatively correlated to the outer radius of curvature of the hood; the length-to-diameter ratio of the EFP projectile is negatively correlated to the radius of curvature of the inner and outer of the hood [30].

As can be seen from Figure 14, for the high strength TiZrTaMoNb high entropy alloy, the EFP molding method is a forward-flip type with relatively small degree of deformation, and the extreme deformation of the pillbox unit did not occur. For this type of molding EFP, the failure parameters of the molding process is relatively small, usually do not use the failure model of the material [24]; and more scholars in the study of the impact of the structural parameters of the polymer charge on the EFP molding process using the failure of the intrinsic model, and achieved more credible results [25-29]. In order to ensure the credibility of each working condition in the subsequent optimization process, it is necessary to add a failure model to the EFP simulation model. Due to the lack of relevant experiments on the failure parameters of TiZrTaMoNb high-entropy alloy, the accurate failure parameters cannot be given. Therefore, the maximum failure stress is roughly estimated by combining Eq. (11) and the strain rate obtained from the simulation results in Fig. 14; the strain rate of TiZrTaMoNb high-entropy alloy in the EFP molding process in Fig. 14 is about 20,562 s-1, and according to the calculation, the maximum failure stress is about 3,525.57 MPa.The material failure model is controlled by using the keywords MAT_ADD_ and MAT_ADD_ in the simulation model. EROSION keyword is used in the simulation model to control the material failure, which is used as the judgment basis for the failure of TiZrTaMoNb high-entropy alloy.

Fixed loading conditions and the wall thickness at the top of the drug mask remain unchanged, and the inner and outer radii of curvature are adjusted according to the above relationship, and the optimized molding effect is shown in Fig. 16, and the densities and LDs are shown in Fig. 17.

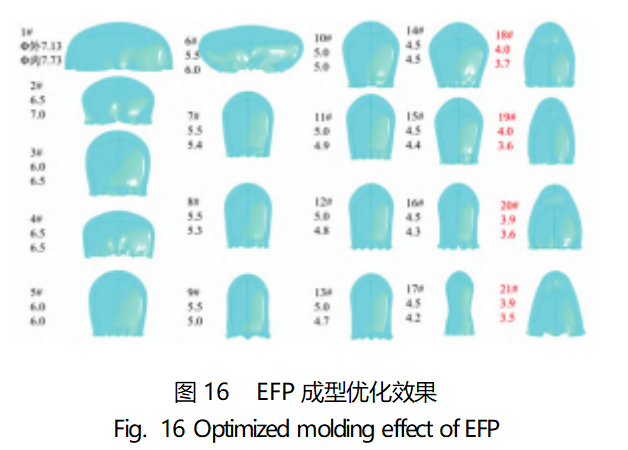
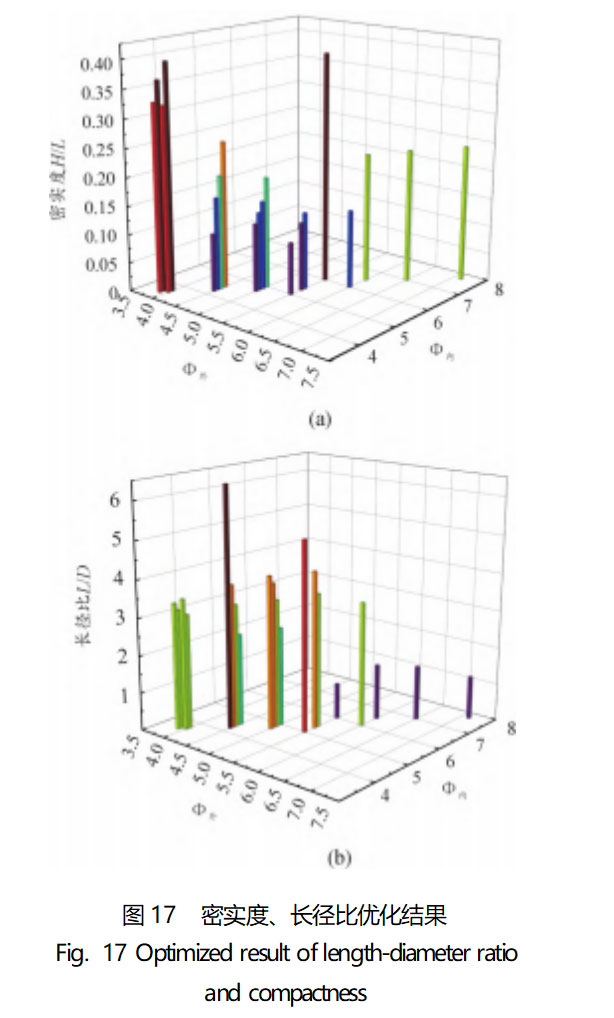
From Fig. 16, it can be seen that by adjusting the inner and outer curvature radius of the pill hood can produce a large change in the EFP shape, and when the inner and outer curvature radius of the pill hood is changed from condition 1# to condition 21#, the denseness and length-to-diameter ratio of the EFP projectile are greatly improved. In Fig. 17(a), comparing the six groups of conditions (Φ outer 6.0cm, Φ outer 5.5cm, Φ outer 5.0cm, Φ outer 4.5cm, Φ outer 4.0cm, Φ outer 3.9cm), it can be found that the compactness increases with the decrease of the outer radius of curvature; and comparing the six groups of conditions, it can be found that the compactness of the EFP decreases with the decrease of the inner radius of curvature. In Fig. 17(b), it can be found that the length-to-diameter ratio of the molded EFP projectile is negatively correlated with both the inner and outer curvatures. The above change relationship is consistent with the law summarized in the literature [30].

From the above optimization process, it can be proved that by adjusting the radius of curvature inside and outside of the flux hood, the EFP projectile length-to-diameter ratio and head compactness can be improved. And the material did not fracture during the EFP molding process and showed good ductility. Among the 21 conditions, the EFP projectiles molded in conditions 18#, 19#, 20# and 21# are better, of which condition 18# (compactness of 0.4, L/D ratio of 3.06) is closer to that of copper in Fig. 15 (compactness of 0.42, L/D ratio of 4.40), which verifies the feasibility of TiZrTaMoNb high-entropy alloy used as EFP.

5 Conclusion 

Static and dynamic compression tests were carried out on TiZrTaMoNb high-entropy alloy using a universal testing machine and a separated Hopkinson press bar. The Johnson-Cook model parameters were fitted according to the test data, and the validity of the fitted parameters was verified using LS-DYNA numerical simulation software. Based on the fitted parameters, an EFP model with a charge diameter of 7.5 cm was selected to verify the feasibility of TiZrTaMoNb high-entropy alloy for use in the EFP drug mask. The following conclusions were obtained.

1) The yield strength, modulus of elasticity and stress-strain relationship of TiZrTaMoNb high-entropy alloy at room temperature were obtained by static compression test. The material has high strength under static conditions, and the yield strength is about 859MPa; the dynamic compression test shows that there is a strain rate strengthening effect in the material, and the yield strength increases with the strain rate.

2) The Johnson-Cook intrinsic model was selected, and some parameters were obtained by fitting using the test data. Based on the SHPB test, a 1/4 symmetric model was established to verify the fitted parameters. The simulation results show that the fitted parameters can reflect the stress-strain relationship of the material in the range of strain rate 851-2403s-1.

3) The simulation model of EFP with a charge diameter of 7.5cm is selected, and by adjusting the radius of curvature inside and outside of the drug mask, the EFP projectile with a better length-to-diameter ratio and head densification can be obtained, which verifies the feasibility of the TiZrTaMoNb high-entropy alloy used as an EFP combat part.

Reference: Liu Jianqing, et al:Study on dynamic properties and application of TiZrTaMoNb high entropy alloy 

TiZrTaMoNb high entropy alloy powder prepared by Stardust Technology using RF plasma spheronization technology has high sphericity, low oxygen content, uniform particle size distribution, etc., and excellent mobility (Hall flow rate ≤standard value), which is suitable for 3D printing (e.g., SLM/EBM), thermostatic compression and other process. The powder exhibits high strength, creep and corrosion resistance at high temperatures, and is mainly used in aerospace (turbine blades, combustion chambers), medical devices (orthopedic implants), and the nuclear industry. Compared with traditional methods, it has no electrode contamination, good batch stability, cost reduction of 30%-40%, and can replace imported high-end powders.